How to Calculate the Volume of a Square Pyramid?

"Man fears time, time fears Pyramids" this old Arab proverb best describes these bizarre yet marvellous structures. Also, you may only be familiar with the Pyramid of Giza. This manufactured marvel was once the tallest building in the world.

Besides, Pyramids are also a math wonder. Did you know that square pyramids closely embody the golden ratio? Now, what is meant by the golden ratio, you wonder? 

"In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. - Wikipedia"

However, you clicked this blog to learn how to find the volume of a square pyramid. So, this blog is your step-by-step guide to learning the calculation method.

What Is a Square Pyramid?

It has a square as the foundation, and four triangular faces come together at a single point. Additionally, it is a three-dimensional geometric shape (called vertex or vertices). It has five faces, which gives it the name pentahedron.

However, pieces of evidence exist that prove the pyramid's design may represent these mathematical and geometric foundations:

• Pi, the circle's circumference is related to its diameter.
• Golden Ratio is visible everywhere in nature, also called Phi.
• The Pythagorean Theorem is expressed as a² + b² = c².

Lastly, regardless of the figure's complexity, it is quite easy to find its volume. The formula for calculating the square pyramid's volume and a step-wise guide are discussed in the following sections.

Did you know that one of the Egyptians' earliest pyramids may be seen near Saqqara? It appears to have been built about over four thousand years ago. It was built as Djoser's tomb and possessed step-sides and a flat top.

University-level academic writing is challenging. Your high school knowledge might not cut it to the college level academically. So, you must get maths assignment help from professional academic writers. Fill out the enrollment form to get in touch with an academic expert. Also, you get free academic resources when you enrol, so enrol today. 

What Are The Steps to Find the Volume of a Square Pyramid?

It is made up of a square base and triangular slope sides that meet at a single point (apex) above the base. Hence, it is a three-dimensional solid. So, the formula for the volume of a square pyramid is as follows, assuming that is the length of one of the square base's sides and 'h' is the height of the pyramid (the distance at right angles between the base and the point):

V=1/3*s2h

Moreover, this formula applies to any square pyramid, whether the size of a paperweight or greater than the Great Pyramid of Giza. Also, you can calculate the volume by utilising the pyramid's "slant height." Simply follow these steps:

• Step 1: First, take note of the pyramid's measurements, such as its base area and height, based on the data provided.

• Step 2: Second, multiply the base area by the height and (1/3).

• Step 3: Third, note down the final answer with the correct measurement units.

• Step 4: Example- 

If a mini square pyramid model whose side is a=6cm, and height h=9cam, the volume is:

Square Pyramid's Volume = 1/3 × a2 × h.

Putting in the value of a and h, we get

The square pyramid's volume = 1/3 × 62× 9

= 1/3 × 36 × 9

= 108.

Hence, the volume of the model is 27 inches3.

Finally, you know how to calculate the volume of the square pyramid. Hopefully, this example guides you through calculating the volume of the square pyramids of any dimensions yourself. Also, there are several online calculators to find the volume of a square pyramid.

How to Use a Square Pyramid Volume Calculator?

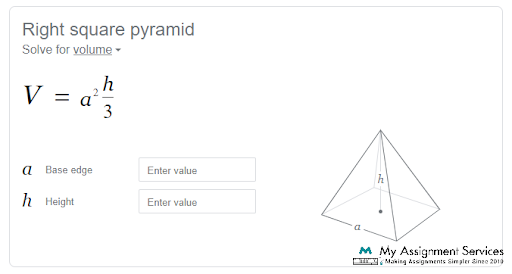
Furthermore, this Google calculator is your best option to find the volume of a pyramid with a square base. All you need to do is enter any two measurements of your square pyramid into our calculator. 

Once you've done that, this calculator will provide you with the volume of your square pyramid. However, sometimes, we cannot measure a or h. Say something that obstructs us from doing so. 

In mathematics, "volume" is the measure that indicates how much a thing or a closed surface occupies three-dimensional space.

But instead, we can measure or have at least one of the values for the slant height (s) and lateral edge to calculate the volume. So, if the height is H and the lateral edge is d, this is the formula to calculate:

V = 2 * (d² - H²) * H / 3.

In some other scenarios, we may lack the measurements mentioned above to quickly find a square pyramid's volume. Good thing we can derive those measurements using the different surface areas of our pyramid.

What is a real-life implication of volume calculations of square pyramids?

Lastly, the most obvious square pyramids to consider are the Giza Pyramids, but the Louvre Museum in Paris is another well-known example. So, there's a prospect of calculating the volume of these amazing square pyramids.

The Great Pyramid of Giza is 481 feet tall. Also, it was the world's highest edifice for 3,800 years! The Lincoln Cathedral in Lincoln, England, finished in 1311, was the first structure taller than the Great Pyramid.

Hence, to put our knowledge into further use, here's how to find the volume of The Great Pyramid of Giza:

Originally, including its smooth limestone casing, the Great Pyramid had a height of 146.7 m (481.4 ft) and a base edge length of 230.6 m (756.4 ft). So, using these values and the square pyramid volume, we obtained its volume, V = 230.6² × 146.7 / 3 = 2600324.004 m³ ≈ 2.6 million m³.

In conclusion, the formula accurately calculates mini to a life-sized square pyramid's volume. We can quickly determine a square pyramid's volume using the earlier formula. 

When you enter university, you will face issues adapting to the assignment. Especially, all the complex concepts might not be your cup of tea so ensure you have maths assignment help from professionals that assist you through all your assignments regardless of the discipline. 

Hence, you may book assignment help via our enrollment form. Fill out the form to get assessment answers for free. Enrol today!